A. Laadhari; H. Temimi;

Efficient finite element strategy using enhanced high-order and second-derivative-free variants of Newton’s method. Applied Mathematics and Computation, Elsevier. Volume 486, 129058 (2025).

DOI https://doi.org/10.1016/j.amc.2024.129058

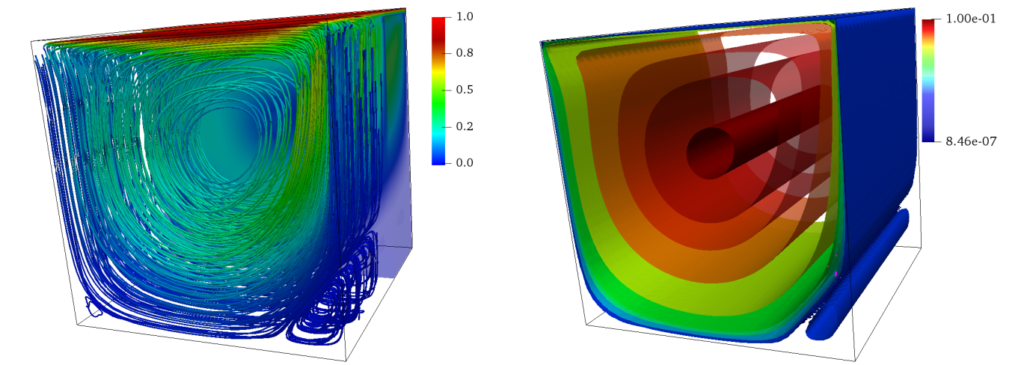
In this work, we propose a stable finite element approximation by extending higher-order Newton’s method to the multidimensional case for solving nonlinear systems of partial differential equations.
This approach relies solely on the evaluation of Jacobian matrices and residuals, eliminating the need for computing higher-order derivatives. Achieving third and fifth-order convergence, it ensures stability and allows for significantly larger time steps compared to explicit methods. We thoroughly address accuracy and convergence, focusing on the singular p-Laplacian problem and the time-dependent lid-driven cavity benchmark. A globalized variant incorporating a continuation technique is employed to effectively handle high Reynolds number regimes. Through two-dimensional and three-dimensional numerical experiments, we demonstrate that the improved cubically convergent variant outperforms others, leading to substantial computational savings, notably halving the computational cost for the lid-driven cavity test at large Reynolds numbers.