Article 28
Stabilized weak-gradient discontinuous finite elements with optimal error estimates for second-order elliptic PDEs
Laadhari, Aymen « Stabilized weak-gradient discontinuous finite elements with optimal error estimates for second-order elliptic PDEs, » Mathematical Modelling and Numerical Simulation with Applications: 5: 3, 644-680, 2025.
ABSTRACT:
This work introduces an accurate finite element approach employing a new stabilized discrete weak gradient, designed for second-order elliptic problems on arbitrary meshes.
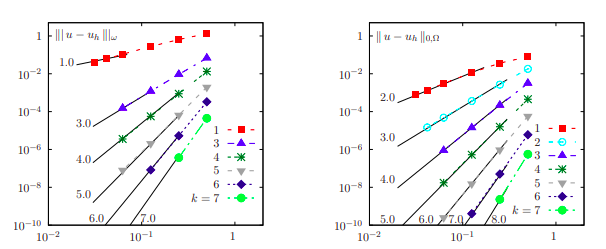
We formulate the approach within a discontinuous Galerkin framework and derive a consistent and coercive bilinear form. Appropriate error analysis on a model problem confirms optimal convergence.
Building on the core analysis, we extend the method to more challenging settings, including time-dependent heterogeneous scenario and a biophysically realistic optimal-control model of photobleaching in the endoplasmic reticulum of budding yeast.
We further illustrate the versatility of the weak-gradient construction by applying it to an unsteady level–set equation relevant to multiphase flow modeling. The implementation supports high-order polynomial spaces, varied boundary conditions, and parallel execution with both direct and iterative linear solvers.
Numerical experiments in 1D, 2D, and 3D are consistent with the theoretical error estimates and demonstrate optimal convergence.
